一、实验目的

1. 掌握周期信号的傅立叶级数分析理论；

2. 掌握带通滤波器的滤波特性；

3. 掌握一般周期信号在时域上的合成方法。

二、实验仪器

1. Ground

2. 交流电压源

3. 普通电阻

4. 三端虚拟放大器

5. 八通道示波器

三、实验原理

在信号的傅立叶级数分析理论中，一个非正弦周期函数可以用一系列频率成整数倍的正弦函数来表示，其中非正弦具有相同频率的成份称为基波或一次谐波，其它成份则根据其频率的2、3、4、...、n等倍数分别称二次、三次、四次、...、n次谐波，其幅度将随谐波次数的增加而减小，直至无穷小。如下图1所示，基频与谐波的幅度与信号的特性紧密相关。

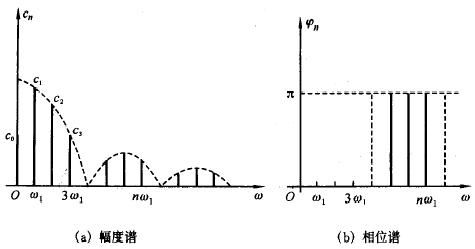
图1  一般周期信号的幅度谱和相位谱

从上图中可以看出，一般周期信号，其谐波幅度随着谐波次数的增加相应该频点信号幅度会减少。因而，对于一个周期信号，可以通过一组中心频率等于该信号各谐波频率的带通滤波器，获取该周期信号在各频点信号幅度的大小。而非周期信号包含了从零到无穷大的所有频率成份，每一频率成份的幅度均趋向无限小，但其相对大小是不同的。

信号通过一个选频网络可以将信号中所包含的某一频率成份提取出来。对周期信号的分解，可以采用性能较佳的带通滤波器作为选频网络。若周期信号的角频率为w₀，则用做选频网络的N种带通滤波器的输出频率分别是ω₀、2ω₀、3ω₀、...、Nω₀,从每一个带通滤波器的输出端可以用示波器观察到相应谐波频率的正弦波，这些正弦波即为周期信号的各次谐波。把分离出来的各次谐波重新加在一起，这个过程称为信号的合成，因此信号的分解及合成的实验装置如图2所示，图中BPF1~BPF9为调谐在基波和各次谐波上的带通滤波器，可分解出方波信号的基波和各次谐波，加法器用于信号的合成。

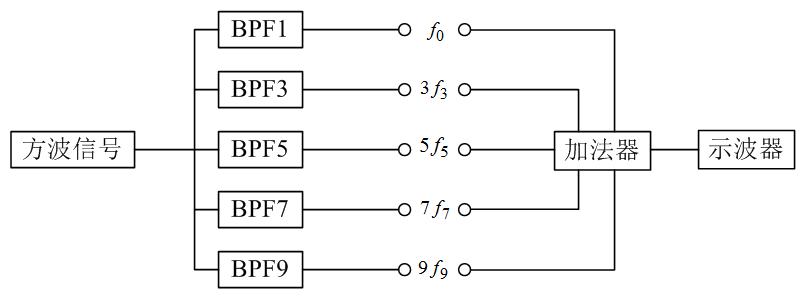
图2 信号的分解与合成实验原理方框图

方波信号按照傅里叶级数可以分解为：

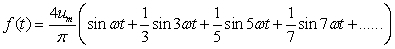
方波信号由1、3、5、7、9等奇次波构成。由公式（1）可知，方波的1~7次谐波的幅度比应为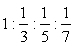，其中奇次谐波的相位与基波相同，只要选择符合上述规律的各次谐波组合在一起，便可以近似合成相应的方波。很显然，随着谐波的增多合成后就越接近方波，但是这与方波还有一定的差距，从理论上来讲，按该方式由无穷多项满足要求的谐波就可逼近方波了。