一、实验目的
1.掌握无源和有源滤波器的滤波特性;
2.掌握带通滤波器的幅频特性曲线;
3.推导带通滤波器的系统函数。
二、实验仪器
1.Ground
2.交流电压源
3.普通电阻
4.普通电容
5.交流电压表
6.波特图分析仪
三、实验原理
1.滤波器简介
滤波器是对输入信号的频率具有选择性的一个双口网络,它允许某些基本频率(通常是某个频带范围)的信号通过,而其它频率的信号受到衰减或是抑制,这些网络可以是由RLC元件或RC元件构成的无源滤波器,也可以是由RC元件和有源器件构成的有源滤波器。
根据幅频特性所表示的通过或阻止信号频率范围的不同,滤波器可分为低通滤波器(LPF)、高通滤波器(HPF)、带通滤波器(BPF)和带阻滤波器(BEF)四种。把能够通过的信号频率范围定义为通带,把阻止通过或衰减的信号频率范围定义为阻带,而通带和阻带的分界点的频率fc成为截止频率或转折频率。
2.滤波器的频响特性定义
滤波器的频响特性H(jω),又称为传递函数或系统函数,如图1所示,它全面反映了滤波器的幅频和相频特性:
图1 滤波器的频响特性定义
滤波器的幅频特性和相频特性为:
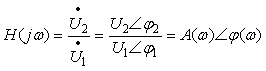
式中, 为滤波器的幅频特性(又称为转移电压比);φ(ω)=φ2-φ1为滤波器的相频特性。可以通过实验方法来测量滤波器的上述幅频特性A(ω)。
为滤波器的幅频特性(又称为转移电压比);φ(ω)=φ2-φ1为滤波器的相频特性。可以通过实验方法来测量滤波器的上述幅频特性A(ω)。
3.带通滤波器
图2为带通滤波器的理想幅频特性,其中Aup为通带的电压放大倍数,fc为截止频率。由图可知带通滤波器的通频带为:BW=(ωH~ωL)=2π(fH~fL)。

图2 带通滤波器的理想幅频特性
图3为常见无源带通滤波器电路。

图3 无源带通滤波器电路
由拉普拉斯变换分析线性电路知电压转移函数H(s)为:

设R1=R2=R,C1=C2=C,则电压转移函数化简为:

根据二阶基本带通滤波器电压转移函数的经典表达式:

可得增益常数K=1,极点频率ωp=1/(RC)和奇偶品质因数Qp=1/3。正弦稳态时,电压转移函数可写成:

幅值函数为:

当ω=ω0=ωp时,ω0称为带通滤波器的中心频率,即:
ω0=ωp=1/(RC)
截止频率ωc是幅值函数自|H(jωp)|纵坐标最大值下降3dB(即 )时所对应的频率。由|H(jω)|的表达式可得:
)时所对应的频率。由|H(jω)|的表达式可得:

对上式求解得:

其中ωch、ωcl分别为上限截止频率和下限截止频率。
通频带宽度BW为:

可见二阶带通滤波器的品质因数Q等于极偶品质因数Qp。Q是衡量带通滤波器的频率选择能力的一个重要指标。
由|H(jω)|的表达式可知:
当ω=0时,|H(j0)|=0;
当ω→∞时,|H(j∞)|=0;
当ω=ω0=ωp=1/(RC)时时,|H(jω0)|=|H(jωp)|=K=1/3,信号频率偏离中心频率越远,幅值函数衰减越大。


