一、实验目的

1. 掌握测试RLC串联谐振电路的幅频特性曲线的方法；

2. 掌握电路发生谐振时的条件及特点；

3. 掌握测量RLC串联谐振电路的截止频率、品质因数和带宽的方法；

4. 掌握电路品质因数对谐振曲线的影响，加深对RLC串联谐振电路频率特性的理解。

二、实验仪器

1. Ground

2. 交流电压源

3. 普通电阻

4. 普通电容

5. 普通电感

6. 交流电压表

7. 交流电流表

三、实验原理

（1）由电感和电容组件串联组成的一端口网络，如图1所示。

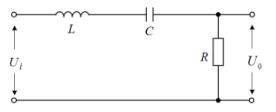
图1  RLC串联电路

该网络的等效阻抗：

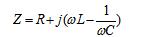
式中，Z是电源频率的函数。当该网络发生谐振时，其端口电压与电流同相位。即：

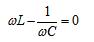
得到谐振角频率：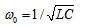

定义谐振时的感抗ω₀L或容抗1/(ω₀C)为特性阻抗p，特性阻抗p与电阻R的比值为品质因数Q，即

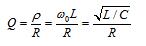
（2）发生串联谐振时，电路的阻抗最小。当端口电压U_i一定时，电路的电流和电阻上的电压均达到最大值，如图2所示，其中电路电流的大小仅与电阻的阻值有关，与电感和电容的值无关；谐振时电感电压与电容电压有效值相等，相位相反。电抗总电压为零，电阻电压等于总电压，电感或电容电压是电阻电压的Q倍，即

U_R0=U_i

U_L0=U_C0=QU_R0

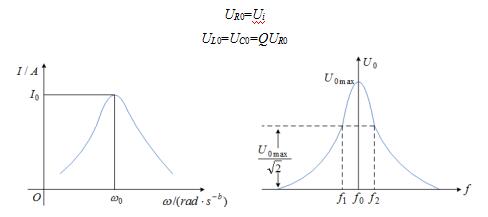
图2  谐振电路的电流和电阻上的电压

（3）RLC串联电路的电流实际电源频率的函数，即：

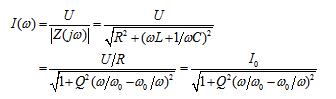
在电路的L、C和信号源U_i不变的情况下，不同的R值得到不同的Q值。对应不同Q值的电流幅频特性曲线如图3(a)所示。为了研究电路参数对谐振特性的影响，通常采用谐振曲线。对上式两边同除以I₀作归一化处理，得到通用频率特性：

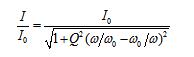
与此对应的曲线称为通用谐振曲线。该曲线的形状只与Q值有关。Q值相同的任何R、L、C串联谐振电路只有一条曲线与之对应。图3(b)绘出了对应不同Q值的通用谐振曲线。

通用谐振曲线的形状越尖锐，表明电路的选频性越好。定义通用谐振曲线幅值下降至峰值的0.707倍时对应的频率为截止频率f_c。幅值大于峰值的0.707倍所对应的频率范围称为通带宽。理论推导可得：

△f=f₂-f₁=f₀/Q

由上式可知，通带宽与品质因数成反比。

图3(a) 不同Q值时的电流幅频特性        图3(b) 通用谐振曲线

（4）电路品质因数Q值的两种测量方法，一是根据公式Q=U_L/U₀=U_C/U₀测定，U_C与U_L分别为谐振时电容C和电感L上的电压；另一种方法是通过测量谐振曲线的通频带宽度△f=f₂-f₁，再根据Q=f₀/f₂-f₁求出Q值。式中，f₀为谐振频率，f₂和f₁是失谐时，亦即输出电压下降到最大值的0.707倍时的上、下限频率。Q值越大，曲线越尖锐，通频带越窄，电路的选择性越好。在恒压源供电时，电路的品质因数、选择性与通频带只决定于电路本身的参数，而与信号源无关。