一、实验目的

1. 掌握电信号的采样方法与过程以及信号恢复的方法；

2. 验证抽样定理。

二、实验仪器

1. Ground

2. VSS

3. VCC

4. 普通电阻

5. 普通电容

6. 交流电压源

7. 时钟电压源

8. 增益器

9. N沟道增强型MOS管2N7000

10. 巴特沃斯低通滤波器BLPF_1200

11. 运算放大器UA741CP

12. 四通道示波器

三、实验原理

利用抽样脉冲把一个连续信号变为离散时间样值的过程称为抽样，抽样后的信号称为脉冲调幅（PAM）信号。在满足抽样定理的条件下，抽样信号保留了原信号的全部信息，并且从抽样信号中可以无失真地恢复出原始信号。抽样定理，即采样频率f_s必须大于等于模拟信号最高频率f_H的2倍。抽样定理在通信系统、信息传输理论方面占有十分重要的地位。抽样过程是模拟信号数字化的第一步，抽样性能的优劣关系到通信传输整个系统的性能指标。

(1)离散时间信号可以从离散信号源获得，也可以从连续时间信号抽样而得。抽样信号f_s(t)可以看成连续信号f(t)和一组开关函数s(t)的乘积。s(t)是一组周期性窄脉冲，T_s称为抽样周期，f_s(t)=1/T_s称抽样频率。

对抽样信号进行傅里叶分析可知，抽样信号的频率包括了原连续信号以及无限个经过平移的原信号频率。平移的频率等于抽样频率f_s及谐波频率2f_s、3f_s…。当抽样信号是周期性窄脉冲时，平移后的频率幅度按sinx/x规律衰减。抽样信号的频谱是原信号频谱周期的延拓，它占有的频带要比原信号频谱宽得多。

(2)正如测得了足够的实验数据以后，我们可以在坐标纸上把一系列数据点连起来，得到一条光滑的曲线一样，抽样信号在一定条件下也可以恢复到原信号。只要用一截止频率等于原信号频谱中最高频率f_n的低通滤波器，滤除高频分量，经滤波后得到的信号包含了原信号频谱的全部内容，故在低通滤波器输出可以得到恢复后的原信号。

(3)还原信号得以恢复的条件是f_s>2f_m，其中f_s为抽样频率，f_m为原信号的最高频率。而f_min=2f_m为最低抽样频率，又称“奈奎斯特抽样率”。当f_s≤2f_m时，抽样信号的频谱会发生混叠，从发生混叠后的频谱中无法用低通滤波器获得原信号频谱的全部内容。在实际使用中，仅包含有限频率的信号是极少的。因此即使f_min=2f_m，恢复后的信号失真还是难免的。

(4)为了实现对连续信号的抽样和抽样信号的复原，可用实验原理框图1所示的方案。除选用足够高的抽样频率外，常采用前置低通滤波器来防止原信号频谱宽而造成抽样后信号频谱的混叠。

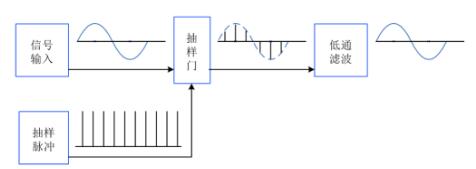
图1  抽样定理实验方框图