一、实验目的

1. 掌握一阶网络的特点及其系统响应特性；

2. 掌握一阶网络波特图的测量方法；

3. 掌握一阶网络阶跃响应的产生方法。

二、实验仪器

1. Ground

2. VSS

3. VCC

4. 普通电阻

5. 普通电容

6. 交流电压源

7. 时钟电压源

8. 运算放大器UA741CP

9. 双通道示波器

10. 波特图分析仪

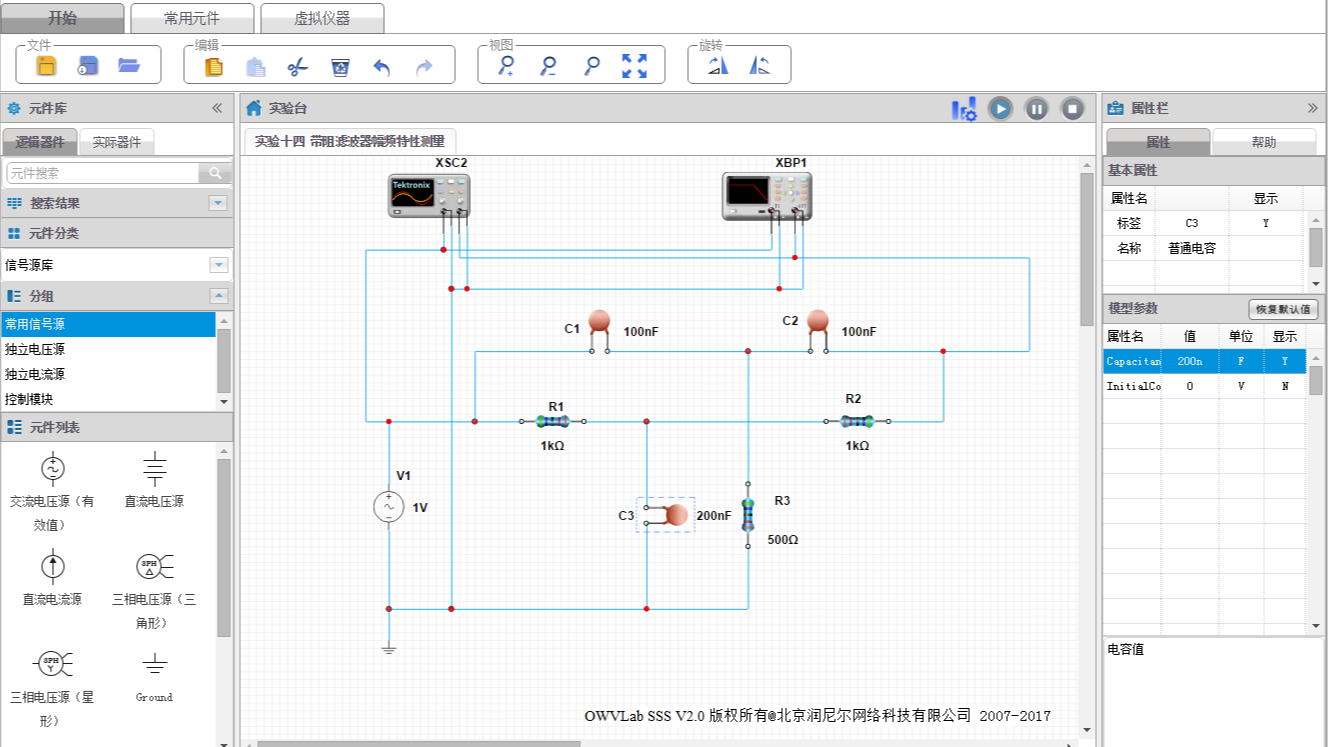
三、实验原理

1.一阶网络特性

系统响应特性是指系统在正弦信号激励下，稳态响应随信号频率变化而变化的特性，称为系统的频率响应特性，简称频响特性。一阶系统是构成复杂系统的基本单元。学习一阶系统的特点有助于对一般系统特性的了解。一阶系统的传输函数一般可以写成：

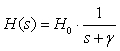
设激励信号x(t)为：

x(t)=E_msin(Ω₀t)

按照系统频响特性的定义可求得该一阶系统的稳态响应为：

y(t)=E_mH₀sin(Ω₀t+φ₀)

其中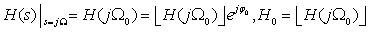

可见，当改变系统输入信号的频率时，稳态响应的幅度和相位也随之而改变。

因果系统是稳定的要求：γ>0，不失一般性可设H₀=γ=1/τ，该系统的频响特性为：H(Ω)=1/(jΩτ+1)。从其频响函数中可以看出系统响应呈低通方式，其3dB带宽点为1/τ。系统的频响特性如下图所示：

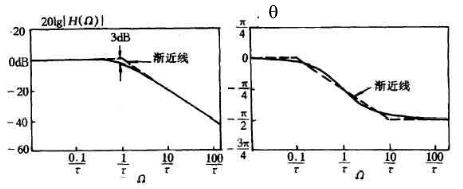
图1 一阶系统频响特性图

一阶系统基本电路如图2所示：

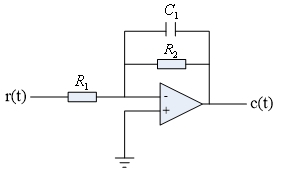
图2 一阶系统基本电路组成

其传递函数为：

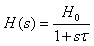
其中H₀=-R₂/R₁，τ=R₂C₁

系统的频响特性为：

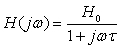
对应的微分方程为

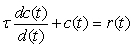
在零初始条件下，利用拉氏变化或直接求解微分方程，可以求得一阶系统在典型输入信号作用下的输出响应。

2. 单位阶跃响应

设系统的输入为单位阶跃函数r(t)=1(t)，其拉氏变换为R(s)=1/s，传递函数为H(s)=1/(1+τs)，则输出的拉氏变换为

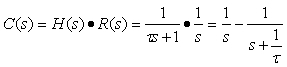
对上式进行拉氏反变换，求得单位阶跃响应为

C(t)=1-e^-t/τ(t ≥0)

上式表明当初始条件为零时，一阶系统单位阶跃响应的变化曲线是一条单调上升的指数曲线，式中的1为稳态分量，-e^-t/τ为瞬态分量，当t→∞时，瞬态分量衰减为零。在整个工作时间内，系统的响应都不会超过起稳态值。由于该响应曲线具有非震荡特性，故也称为非周期响应，一阶系统的单位阶跃响应曲线如图3所示。

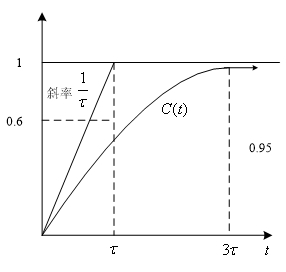
图3 一阶系统的单位阶跃响应图

图中指数响应曲线的初始斜率为1/τ，因此，如果系统保持初始响应的变化速度不变，则当t=τ时，输出量就能达到稳态值。实际上，响应曲线的斜率是不断下降的，经过时间τ后，输出量C(t)从零上升到稳态值的60%，经过3τ时，C(t)将分别达到稳态值的95%。可见，时间常数τ反应了系统的相应速度，τ越小，输出响应上升越快，响应过程的快速性也越好。