一、实验目的
1. 掌握低通无源滤波器的设计;
2. 掌握巴特沃斯低通滤波器的特点;
3. 掌握低通滤波器的系统函数。
二、实验仪器
1. Ground
2. VSS
3. VCC
4. 交流电压源
5. 普通电阻
6. 普通电容
7. 运算放大器UA741CP
8. 波特图分析仪
三、实验原理
1. 模拟滤波器
模拟滤波器根据电路组成组件可分为无源滤波器和有源滤波器两种。无源滤波器由电感L、电容C及电阻R等无源组件组成;有源滤波器一般由集成运放与RC网络构成,它具有体积小、性能稳定等优点,同时,由于集成运放的增益和输入阻抗都很高,输出阻抗很低,故有源滤波器还兼有放大与缓冲作用。利用有源滤波器可以突出有用频率的信号,衰减无用频率的信号,抑制干扰和噪声,以达到提高信噪比或选频的目的,因而有源滤波器被广泛应用于通信、测量及控制技术中的小信号处理。
模拟滤波器根据其通带的特征可分为:(1)低通滤波器;(2)高通滤波器;(3)带通滤波器;(4)带阻滤波器。在这四类滤波器中,又以低通滤波器最为典型,其它几种类型的滤波器均可从它转化而来。
二阶有源滤波器是一种信号检测及传递系统中常用的基本电路, 也是高阶虑波器的基本组成单元。常用二阶有源低通滤波器的电路型式有压控电压源型、无限增益多路反馈型和双二次型。二阶有源低通滤波器由两节RC滤波电路和同相比例放大电路组成,在集成运放输出到集成运放同相输入之间引入一个负反馈,在不同的频段,反馈的极性不相同,当信号频率f>>f0时(f0为截止频率),电路的每级RC电路的相移趋于-90?,两级RC电路的移相到-180?,电路的输出电压与输入电压的相位相反,故此时通过电容C引到集成运放同相端的反馈是负反馈,反馈信号将起着削弱输入信号的作用,使电压放大倍数减小,所以该反馈将使二阶有源低通滤波器的幅频特性高频端迅速衰减,只允许低频端信号通过。其特点是输入阻抗高,输出阻抗低。
对于模拟低通滤波器的设计方法,一般是通过逼近的设计方法。在最常用的滤波器中又以巴特沃思滤波器、切比雪夫滤波器最为常用。
2. 巴特沃斯滤波器
巴特沃斯低通滤波器的频响特性为:
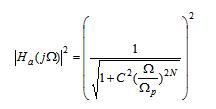
其中C为常数,N为滤波器的阶数,Ω/Ωp为归一化低通截止频率。特点有:(1)最大平坦性:其滤波器在0频点处附近一段范围内是非常平直的,它是以原点的最大平坦性来逼近理想低通滤波器;(2)通带、阻带下降的单调性;(3)具有良好的相频特性;(4)3dB的不变性:随着阶数N的增加,频带边缘下降越陡峭,越接近理想特性。但不管N是多少,幅频特性都通过-3dB点,巴特沃斯低通滤波器的频响特性如图1所示。
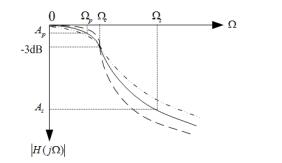
图1 巴特沃斯滤波器的频响特性
滤波器的特性完全由其阶数N决定。当N增加时,滤波器的特性曲线变的更陡峭,这时虽然决定了在Ω=Ωp处的频响函数总是衰减3dB,但是在通带的更大范围内接近于0,在阻带内更迅速的接近于零,因而频响特性更接近与理想的矩形频率特性。
根据给定的通带指标Ωp、Ap和阻带指标Ωs、As,可得:
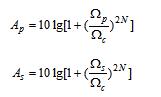
所以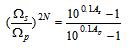 ,则得到滤波器的阶数N为满足下式的最小整数:
,则得到滤波器的阶数N为满足下式的最小整数:
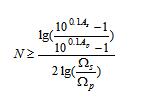
得到了巴特沃斯滤波器的阶数N后,就可以确定平方幅度响应|H(jΩ)|2,利用|H(jΩ)|2可以得到零极点形式的传输函数H(s)。设归一化巴特沃斯低通滤波器的传递函数为H(p),其中p=jλ,则:
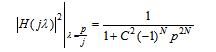
根据设计指标要求λp,αp,λs,αs确定归一化巴特沃斯低通滤波器幅度平方函数中的待定系数C及滤波器的阶数N;然后再根据幅度平方函数确定巴特沃斯低通滤波器的传递函数H(s)。
巴特沃斯滤波器的设计过程:
(1)将实际频率Ω归一化得λp=Ωp/Ωp=1,λs=Ωs/Ωp,由于
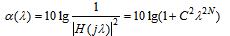
带入λp,αp,λs,αs得
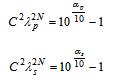
(2)由于λp=Ωp/Ωp=1,因此

其中 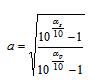 通常取αp=-3dB,即C=1。
通常取αp=-3dB,即C=1。
(3)由于 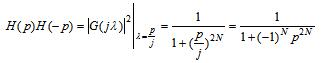
解得极点为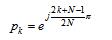 ,k=1,2,L,2N。
,k=1,2,L,2N。
去掉归一化影响,采用归一化频率即λp=Ωp/Ωp=1,就得到截止频率为Ωp的巴特沃斯低通滤波器的系统函数H(p)。


